生命体由于其生物活性而具有独特的性质。从组织器官到构成组织器官的单个细胞，再到细胞内部的多种细胞器和亚细胞结构，每个层级的组成单元都在吸收营养并展开各自的生命活动，以实现特定的生物功能。尽管不同生命系统的内部结构和功能各有不同，但它们都能够吸收能量并将其转化为机械运动。因此，科学家们创造性地将其归为一类，提出活性物质的概念^[1-4]。这些自主运动的个体在邻居及环境的影响下，往往会涌现出更大规模的群体动力学现象。例如大规模定向运动^[5-6]、旋涡^[7-8]以及相分离^[9]等。

生命系统不是单一组成系统，无论是生物体群落与外部环境以及其他种群的相互作用，还是单个生物体内部的组织间的相互影响，往往都会形成物理界面^[10-13]。例如，在鲨鱼的影响下，沙丁鱼群的边界处形成局部界面结构^[14]；斑马鱼体表的不同组织表达不同的色素，形成空间规则分布的条纹，类似于图灵斑图^[15]；在组织尺度下，癌组织和正常细胞组织相互作用，能够产生复杂的界面结构，揭示癌症的恶性程度^[16]。生命系统的复杂性以及环境的多样性常常使得系统在边界和内部产生截然不同的动力学行为、生理功能和命运选择，令整个系统表现复杂非均匀的空间结构特征。因此，为了更好地探究生物界面对于生命系统的影响，常常将生命系统考虑为多相系统，即多种组分共存的系统。

生物界面的研究具有明显的时空动力学特性，因而具有相当的复杂性。首先，细胞组织等生命系统不断将化学能转化为机械运动，细胞间、细胞内部和外部环境的作用力在运动过程中不断变化，并且会引起力敏感的生化信号的激活与传播，这是典型的力学、化学和生物学耦合过程^[17-18]。另外，生物界面的形貌复杂多样，其形貌特征以及演化规律往往能反映出组织的生物特征。因此，研究生物界面的形成以及演化规律，可加深人们对生命过程的理解，也可为一些疾病的诊断和治疗提供思路。

在生命系统中，活性的差异非常普遍，这里的活性一般指的是细胞的运动能力，例如癌变的细胞往往运动能力较弱，但是侵袭能力显著增强^[19]。此外，在伤口愈合的过程中，正常细胞和病变细胞的运动能力也有显著差异。过去的研究往往只关注于生命系统中单一组分的动力学行为，而对于同样广泛存在的双相生命系统的研究，尤其是活性差异引起的生物界面问题，目前尚关注较少。

因此，本文通过构建具有明显活性差异的生物界面，探究活性–非活性系统的界面形貌发生和界面附近的拓扑缺陷动力学行为，并从流场、拓扑缺陷的分布、界面拓扑等方面阐述界面动力学的发生机制。最后，从取向的失稳角度确定拓扑缺陷与界面的相互作用模式，从而确定活性驱动界面演化的物理机制。

1.   研究方法

1.1   活性向列液晶界面连续性理论

液晶是物质存在的一种状态，介于晶体、固体和流体之间，既能够像液体一样流动，同时局部分子又具有一定的取向性^[20]。细胞单层是非平衡系统，每个细胞自己能够消耗能量，持续地变形、运动，具有一部分流体的特性，符合活性液晶理论的要求^[21]。细胞个体的长细比（slenderness ratio）较大，因而存在一定的取向性，具有一部分固体的特性，适合采用活性液晶理论来描述^[22]。实验结果表明，活性液晶理论能够较好地描述细胞单层内复杂的力学行为^[23-25]。

1.1.1   双相理论的能量函数

过去的研究主要集中在单一系统中，没有考虑由两种活性不同的细胞组成的系统，本文首次提出双相理论的概念，并将相场与取向场进行了合理的耦合。

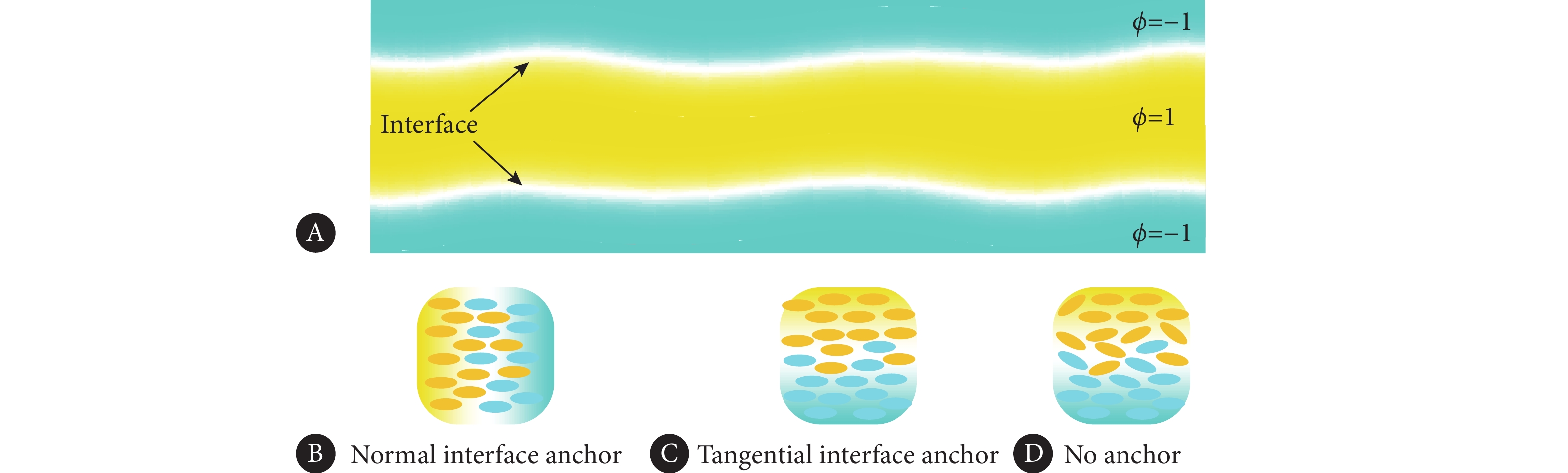
为了描述由两种不同的细胞组成的系统，引入一个标量的场变量$ \phi $，使用$ \phi = 1 $来表示一种细胞，使用$ \phi = - 1 $来表示另一种细胞，而$ \phi = 0 $则对应两种细胞的界面。描述相场$ \phi $的能量函数采用Ginzburg-Landau的能量形式^[26]：

式(1)中，$ {A_\phi } > 0 $，此时第一项表示系统趋近于发生相分离，在$ \phi = \pm 1 $时对应的能量值最小。第二项中$ {K_\phi } > 0 $，表示相场$ \phi $的空间梯度变化并且能够产生一个有限宽度的混合界面。

整个系统是有取向的，取向可以用二阶张量$ {{Q}}{\text{ = }} q(2{{nn}} - {{I}}) $来描述^[22]。其中，q表示有序性的幅值，n表示局部的取向方向，I为单位矩阵。本文系统的两相系统均为有序的，因此，需要考虑将控制相变的系数与相场变量$ \phi $进行合理耦合。结合前人的经验，本文对于液晶能量的耦合形式表示为：

式(2)中，第一项控制单相物质的有序性，通过二次项$ q_{\rm{nem}}^2{\phi ^2} $的引入，使得系统在$ \phi = \pm 1 $时，系统的序参数值趋近于$ q_{\rm{nem}}^{} $，而当$ \phi = 0 $时，即界面位置，系统由于两相物质的混合属性，系统序参数值趋近于0。通过上述的耦合形式， 结合相分离的属性，实现系统中两相物质均具备向列有序性的属性。此外，式(2)中的系数$ {A_Q} $和$ {k_Q} $定义了系统的 特征尺寸，即$\sqrt {\raise0.5ex\hbox{$\scriptstyle {{k_Q}}$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle {{A_Q}}$}}$，表示细胞单层系统中向列液晶属性的相关长度，即拓扑缺陷核的大小。例如，Madin-Darby canine kidney （MDCK）细胞单层和C2C12细胞单层的此特征长度具有显著差异^{[23, 25]}。

细胞间的粘附存在差异，线张力不同，同时还存在细胞的增殖以及生化信号的产生和传递，细胞取向在界面上往往存在明显的偏好性。例如，在感知刚度的作用下，具有明显刚度梯度的界面能够驱动较软的细胞法向排列在界面上^[27]；而在排斥力的作用下，细胞又能够以切向排列的形式存在^[28]。这是生命系统中比较典型的两种排列状态，本文对于界面取向的能量表示为^[29]：

此能量只在界面处起作用，取向的控制由系数$ {L_0} $的符号决定， 因此，对于本文所关注的无限大双相系统，系统的自由能包括三部分，分别为混合自由能$ {F_\phi } $、向列自由能$ {F_n} $和界面自由能$ {F_{\rm{int} }} $：

1.1.2   基本控制方程

整个系统的场变量主要有三个，分别为相场$ \phi $，取向场Q和速度场$ {{v}} $。相场$ \phi $的控制方程为^[26]：

本文中，$ \phi $为保守场，即不考虑细胞增殖和凋亡引起的变化。式(5)中M为扩散系数。其中${{\mu = {\text{δ }}{F_\phi }} \mathord{\left/ {\vphantom {{\mu = {\text{δ }}{F_\phi }} {{\text{δ }}\phi }}} \right. } {{\text{δ }}\phi }}$为有效的化学势，控制物质的守恒。

取向场$ {{Q}} $的控制方程为^[22]：

除了流场产生的平流效应，细胞在运动中会受到速度的梯度效应发生方向的转变，这种变化由共旋项$ {{S}} $来表示：

式(7)中，$ {{\Omega }} $和$ {{E}} $分别是速度梯度张量$ \nabla {{v}} $的对称部分和反对称部分，表示涡量张量和应变率张量。二者对取向场$ {{Q}} $的贡献大小主要由流动参数$ \lambda $表征。

方程中的最后一项描述取向场的松弛动力学，其中$ {\Gamma _Q} $为松弛系数。$ {{H}} $为分子场，定义为：

序参数$ {{Q}} $和相场$ \phi $的演化与速度场v高度耦合。整个系统的密度被认为是常数，即系统为体积不可压，速度场的控制方程为：

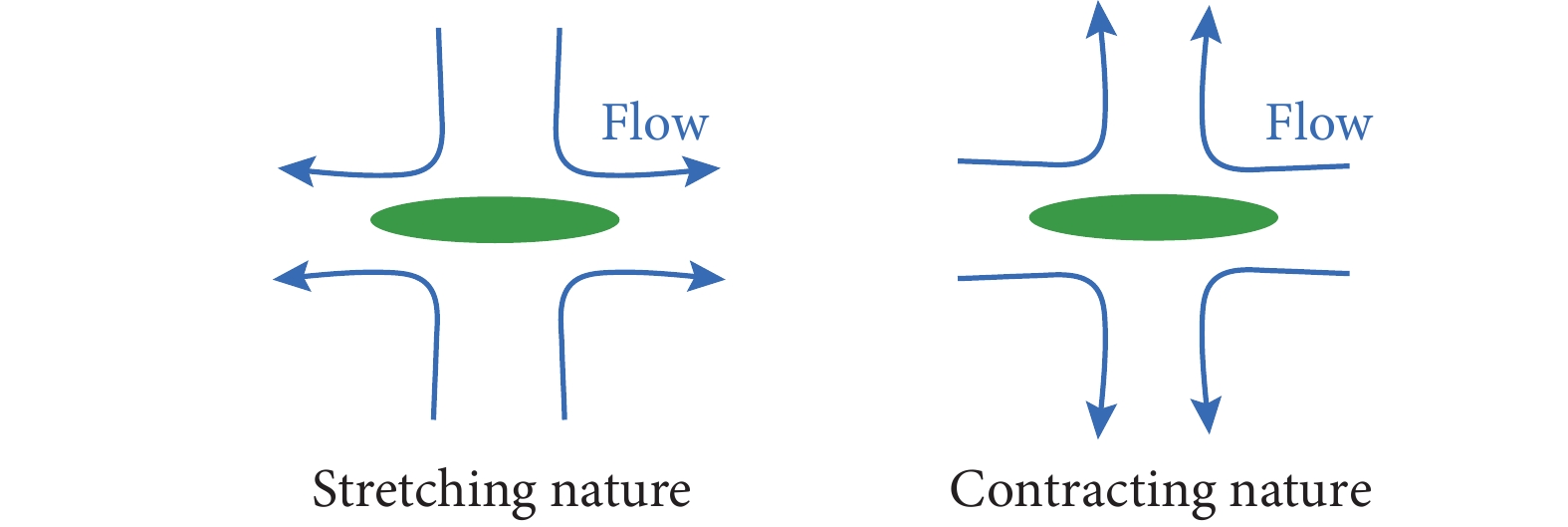
式(10)最后一项表示粘性摩擦力，通常来自于细胞与基底的相互作用，$ \gamma $为摩擦系数^[30]。$ {{\sigma }} $为广义的应力张量，包含主动应力项$ {{{\sigma }}^{act}} = - \overline \zeta Q $，其中$ \overline \zeta = {\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 2$}}\left( {1 + \phi } \right){\zeta _1} + {\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 2$}}\left( {1 - \phi } \right){\zeta _2} $表示局部的平均活性系数，代表着细胞对环境的作用力属性，可以分为推力和拉力，即拉伸活性（细胞推动局部流体）和收缩活性（细胞拉拽局部流体），分别如图1所示。

图  1  细胞与局部流体作用模式

Figure  1.  Interaction patterns between cells and the local fluid

下载: 全尺寸图片 幻灯片

1.2   拓扑缺陷动力学

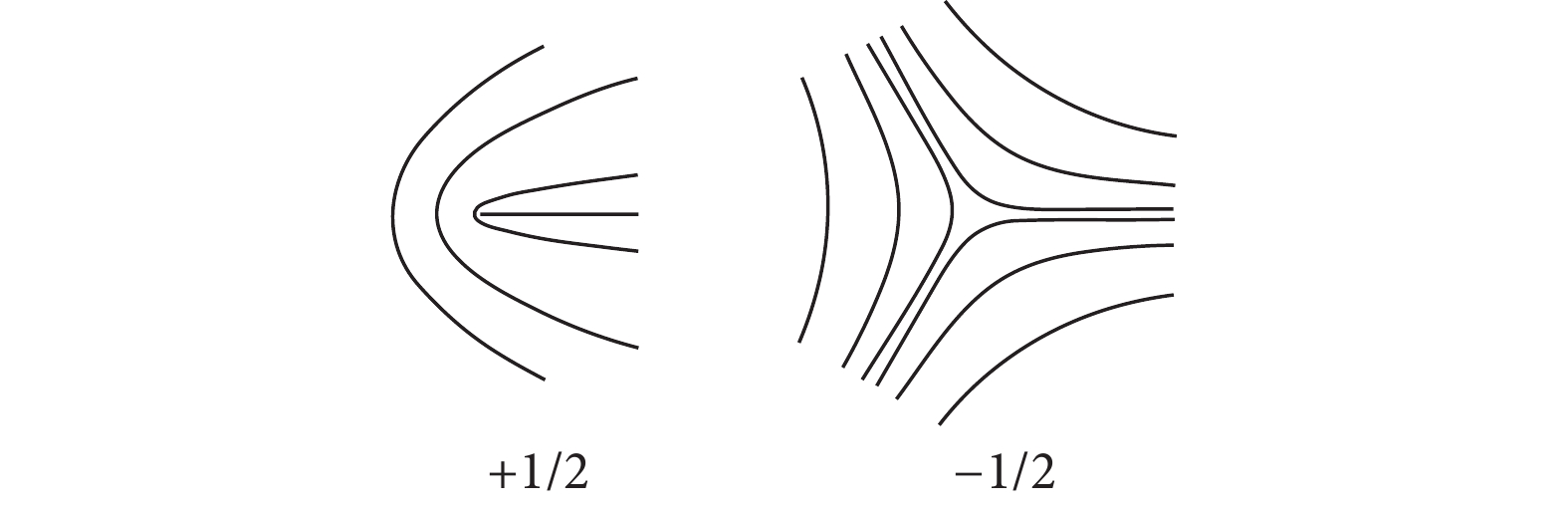
由于生命系统具有活性，细胞源源不断地从环境中吸收能量，转化为细胞的形变或迁移运动，局部的取向场Q会受到局部速度场的影响，同时也会伴随局部取向的非均匀状态，生成拓扑缺陷。细胞单层中主要有两种拓扑缺陷，如图2所示，分别为彗星形状的+1/2拓扑缺陷和三叶草形状的−1/2拓扑缺陷。+1/2拓扑缺陷是极性结构，具有一个极轴，−1/2拓扑缺陷的结构具有三倍对称性。

图  2  细胞单层中常见拓扑缺陷示意图

Figure  2.  Schematic diagram of common topological defects in the cell monolayer

下载: 全尺寸图片 幻灯片

在被动系统中，拓扑缺陷类似于电荷，同种电荷的拓扑缺陷互相排斥，异种电荷的拓扑缺陷互相吸引，因而系统从无序向有序不断转变，不断发生缺陷对的融合湮灭。然而，由于生命系统的活性，拓扑缺陷表现出和被动系统截然不同的动力学行为^[30]。对于±1/2拓扑缺陷，GIOMI等^[30]通过求解斯托克斯方程，得到缺陷核半径R附近的流场表达式，确定了±1/2拓扑缺陷的运动形式。+1/2缺陷沿着其对称轴以常速度$ {\raise0.5ex\hbox{$\scriptstyle {\zeta R}$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle {4\eta }$}} $匀速前进，速度与活性系数$ \zeta $呈线性关系，而−1/2缺陷的推进速度为0，不能够发生自主的运动。SAW等^[25]采用MDCK细胞进行了二维实验，通过对MDCK细胞单层的运动进行表征，结合细胞单层的速度场形式与+1/2拓扑缺陷的运动轨迹，发现具有较强细胞间粘附的MDCK细胞单层呈现出拉伸活性的向列液晶性质。

1.3   双相向列系统

建立如图3所示的双相向列系统，其中，相场变量$ \phi = 1 $和$ \phi = - 1 $分别表示两种不同的向列系统，$ \phi = 0 $为向列界面。由于界面的存在，细胞在界面上的取向受到影响，往往会产生沿着特定方向排列的行为，本文只考虑在实验中观察到的比较典型的排列模式，分别为无锚定、法向锚定和切向锚定三种模式。对于初始是直线型的界面，这里假设取向场$ {{Q}} $随机分布，速度场$ {{{v}}_0} = 0 $。三种变量均满足周期性边界条件，即对应无限大区域的情况。对界面两侧的两种组分，认为其中一种是具有活性的，而另一种没有活性，即$ \phi = 1 $对应$ {\zeta _1} \ne 0 $，$ \phi = - 1 $对应$ {\zeta _2} = 0 $。

图  3  活性-非活性界面模型

Figure  3.  A model of the active-inactive interface

下载: 全尺寸图片 幻灯片

1.4   数值计算方法

本文使用针对速度场的格子玻尔兹曼方法^[31]和针对相场和取向场的有限差分离散方法^[32]，采用显式的欧拉向前积分的形式离散场变量的导数，编写了MATLAB程序进行数值求解。考虑到计算的效率问题，对于导数计算过程，采用C++进行编程计算，这种MATLAB和C++混合编程的方式，不仅提高了计算效率，同时对数据的处理较为简便、快捷。

1.5   界面几何特征统计方法

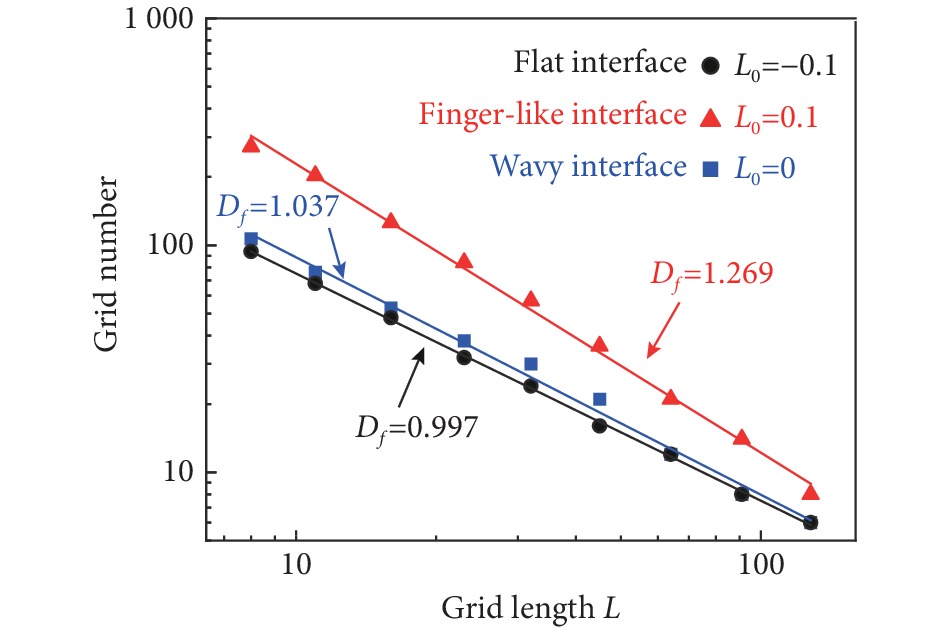
采用分形维数对界面局部的几何复杂度进行表征^[33]，分形维数采用格子计数的方法来计算。对于不同的格子边长L，计算包含界面的格子数量n， 格子数量n和格子边长L满足关系$ n(L) = {L^{ - {D_f}}} $, 其中，$ {D_f} $为界面的分形维数。

1.6   参数无量纲化

计算中的参数均以格子玻尔兹曼单位为基础，长度尺度的无量纲基本单位为$ \Delta L = 1$ μm，时间尺度的无量纲基本单位为$ \Delta t = 10 $ ms，力尺度的无量纲基本单位为$ \Delta F = 20 $ pN。采用的无量纲参数见表1。

表  1  模拟程序使用的关键参数数值

Table  1.  Key parameter values used in simulations

Parameter	Symbol	Simulation value	Physical value and reference
Mixture free energy coefficient	$ {A_\phi } $	0.2	Reference[34]
Interface elastic stiffness	$ {k_\phi } $	0.35	Reference[34]
Array 1 free energy coefficient	$ {C_1} $	0.05	Reference[32, 35]
Array 2 free energy coefficient	$ {C_2} $	0.05	Reference[32, 35]
Elastic constant 1	$ {K_{Q1}} $	0.05	1 pN[32, 35-36]
Elastic constant 2	$ {K_{Q2}} $	0.05	1 pN[32, 35-36]
Alignment parameter	$ \lambda $	0.7	Reference[37]
Equilibrium order parameter value	$ {q_{\rm{nem}}} $	1	1[22]
Friction coefficient	$ \gamma $	0.1	1e−4 nN·s/μm4[38]
Shear viscosity	$ \eta $	1/6	0.0333 Pa∙s[35-36]
Density	$ \;\rho $	40	Reference[32-33, 39]
Array 1 activity coefficient	$ {\zeta _1} $	0.02	0.4 Pa[35-36]
Array 2 activity coefficient	$ {\zeta _2} $	0	0 Pa

下载: 导出CSV 

| 显示表格

2.   结果

2.1   活性–非活性向列液晶界面形貌发生

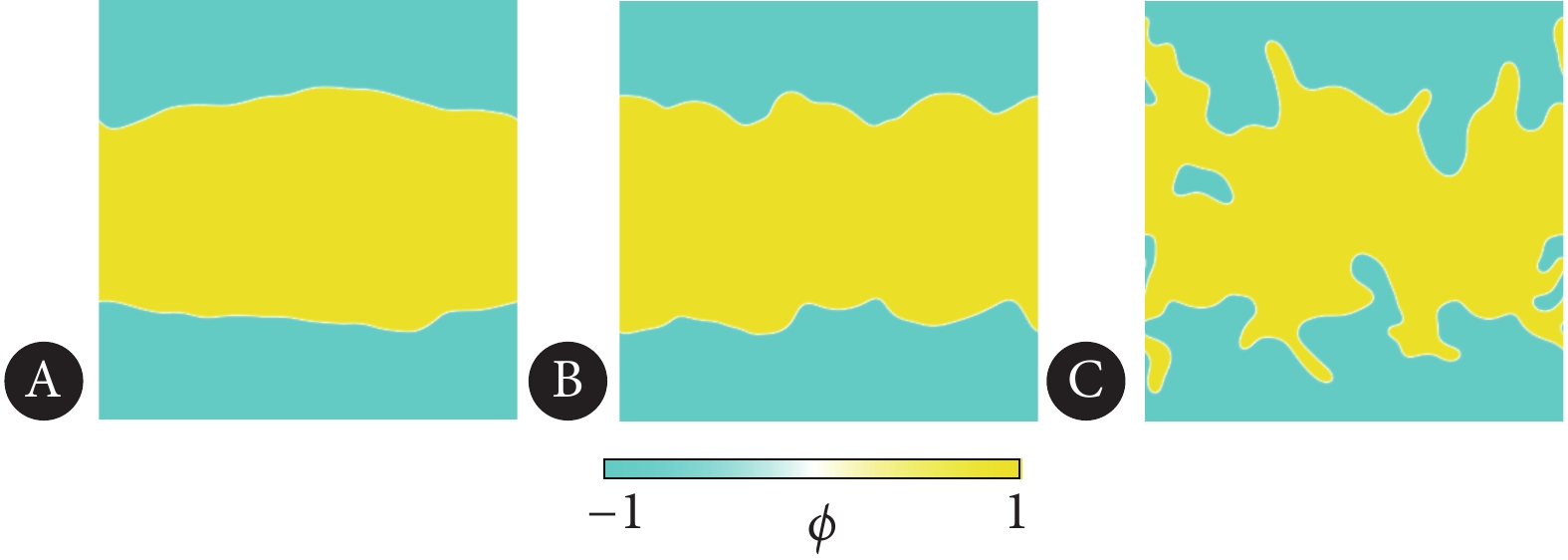
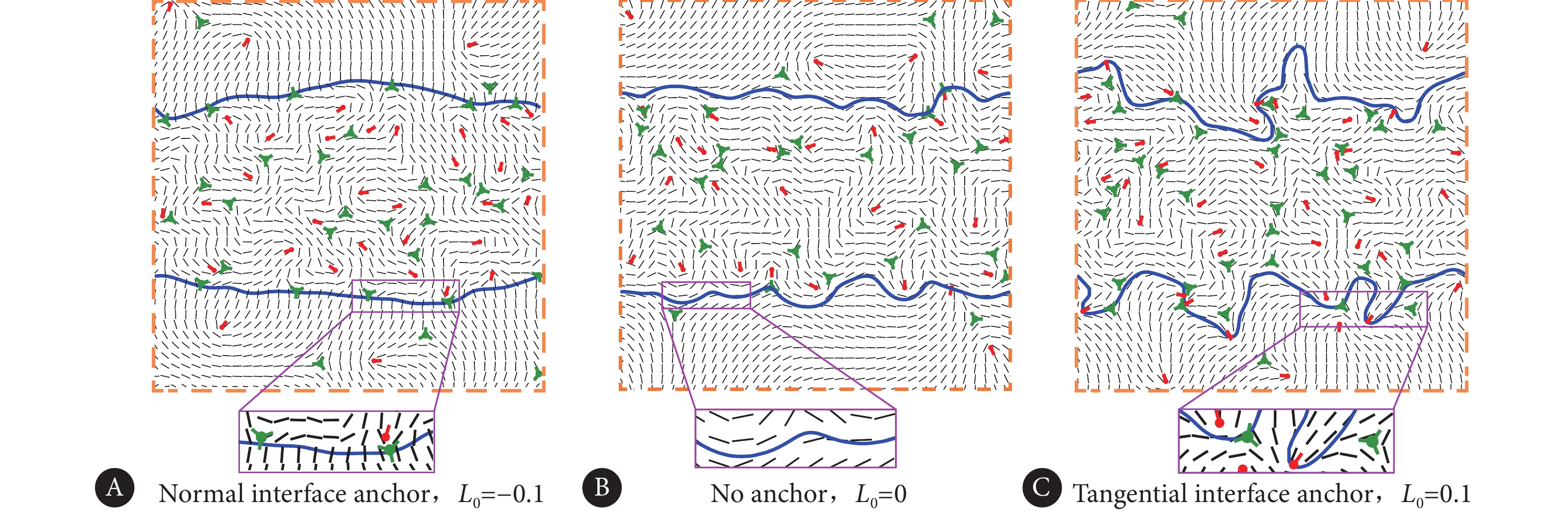
在细胞单层中，生物界面的演化主要由细胞的速度场驱动，对于不同的界面锚定约束$ {L_0} $，计算结果表明，在拉伸活性$ {\zeta _1} = 0.02 $的作用下，界面主要产生三种典型的形貌。分别为直界面，波浪形界面和指形界面，如图4所示。对于法向锚定条件，即$ {L_0} = - 0.1 $，界面比较稳定，如图4A所示。相比之下，无界面锚定条件下（$ {L_0} = 0 $），界面局部形成较大的波动，如图4B所示。而在切向的界面锚定条件下（$ {L_0} = 0.1 $），初始的直线界面十分不稳定，局部有大量指形结构形成，这种指形结构不断生长，向非活性区域延伸，界面形貌变得混乱，如图4C所示。

图  4  三种典型的界面形貌

Figure  4.  Three typical interface morphologies

A, Flat interface; B, wavy interface; C, finger-like interface.

下载: 全尺寸图片 幻灯片

对界面的几何分形维数进行计算，结果如图5所示。可以发现，对于直界面，分形维数$ {D_f} $接近于1（$ {D_f} = 1 $为标准直界面的分形维数），表明界面局部的光滑度较高，界面比较规则。而对于波浪形界面， 其分形维数为$ {D_f} = 1.037 $，比直界面的分形维数稍大，进一步表明界面的局部结构比直界面更加复杂，如图4所示。最后，对于指形界面，其界面的长度、波动程度、复杂度均比较高，对应的分形维数最大。

图  5  三种典型界面形貌的分形维数

Figure  5.  Fractional dimensions of the three typical interface morphologies

下载: 全尺寸图片 幻灯片

2.2   界面拓扑影响界面处的有序性及排列方式

生物界面拓扑会影响界面的取向场排列模式，进而对序参数有重要作用。对于均匀的界面，在切向排列（$ {L_0} > 0 $）的作用下，假设其相场浓度$ \phi $沿着x轴均匀分布，只沿着y方向从$ \phi = - 1 $向$ \phi = 1 $变化，即$ {\phi _{,x}} = 0 $。对于均匀的取向场，其取向分量可以表示为：

因此，其自由能最小状态下对应的分子场可以表示为：

其能量最小状态下序参数为：

类似地，在法向排列（$ {L_0} < 0 $）作用下，序参数表示为：

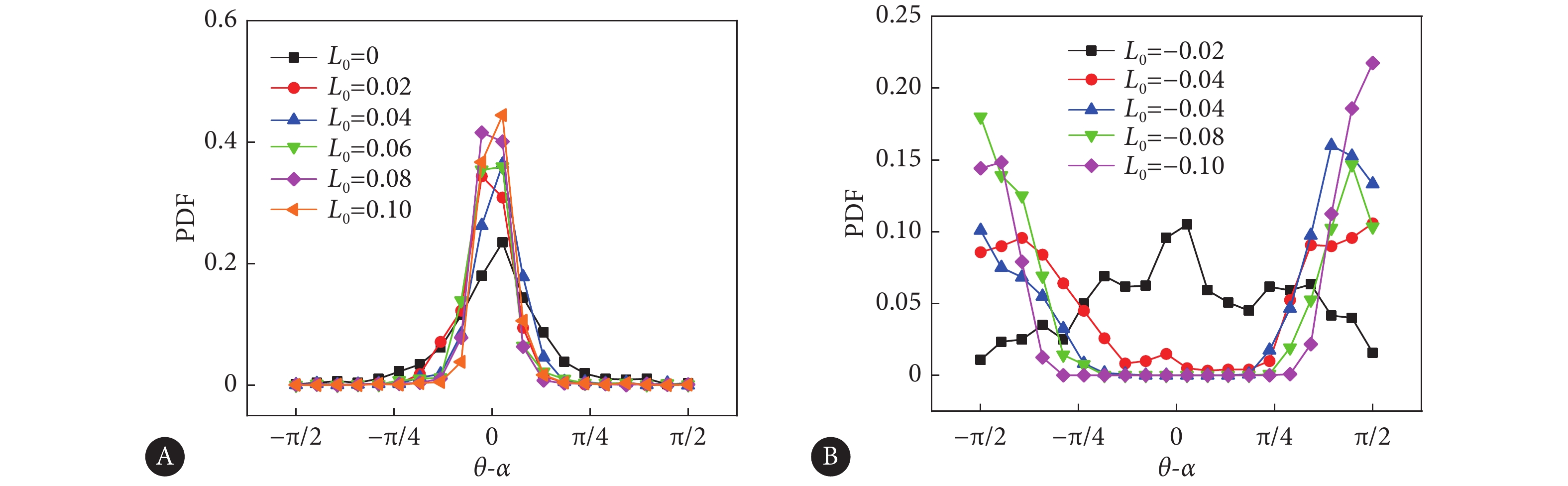
这反映了界面锚定作用对序参数的影响情况，即界面的排列拓扑增强了界面的有序性。细胞取向场在界面处的排列受其本征活性的控制，这种控制可被界面拓扑作用增强、削弱甚至逆转。用$ \theta $表示界面处取向场的方向，用$ \alpha $表示界面的切向方向。因此，$ \theta - \alpha $表示取向场与界面切向的偏离程度，$ \theta - \alpha = \pm \dfrac{\pi }{2} $表示取向场与界面切向垂直，为法向排列；$ \theta - \alpha = 0 $表示取向场与界面切向平行，为切向排列。图6表示不同界面锚定条件下$ \theta $和$ \alpha $偏离的概率密度分布情况。从图6A可以发现，对于无界面锚定情况（$ {L_0} = 0 $），界面上的取向场呈现出切向排列，此时该排列效应是由于细胞单层的拉伸活性（$ {\zeta _1} = 0.02 $）导致，即活性引起的界面锚定^{[34, 38]}。在界面切向拓扑的作用下（$ {L_0} > 0 $），该排列模式不变。而对于法向界面锚定约束下（$ {L_0} < 0 $），当约束作用较小时（$ {L_0} = - 0.02 $），此时概率密度分布（PDF）呈现出比较均匀的形态，最大值发生在$ \theta - \alpha = 0 $，此时是活性与界面约束竞争的作用。如果进一步增大界面约束的强度，界面处则是约束作用占据主导，最大值对应$ \theta - \alpha = \pm \dfrac{\pi }{2} $，呈法向排列模式。

图  6  界面处取向场排列的概率密度分布

Figure  6.  Probability density function (PDF) of the orientational field arrangement at the interfaces

A, Tangential interface anchor; B, normal interface anchor.

下载: 全尺寸图片 幻灯片

2.3   拓扑缺陷分布的不均匀性

通过对界面上的拓扑电荷数进行统计计算，发现对于活性-非活性的细胞单层界面系统，界面的拓扑电荷数受到界面锚定性质的显著影响。图7反映了三种界面处的缺陷分布情况，从中可以看出，对于法向锚定的情况（$ {L_0} = - 0.1 $），界面处间隔分布着−1/2拓扑缺陷。

图  7  三种界面处的取向场及缺陷分布

Figure  7.  The orientation field and topological defect distribution at the three types of interfaces

A, Normal interface anchor and aggregation of −1/2 topological defects; B, neutrally-charged unanchored interface; C, tangential interface anchor and aggregation of +1/2 topological defects.

下载: 全尺寸图片 幻灯片

另外，对于无锚定情况（$ {L_0} = 0 $），界面几乎呈现出一种电中性的带电形态。在切向锚定的约束下（$ {L_0} = 0.1 $），在界面局部曲率较小处，主要分布−1/2拓扑缺陷；而在曲率较大的界面位置，主要分布+1/2拓扑缺陷。

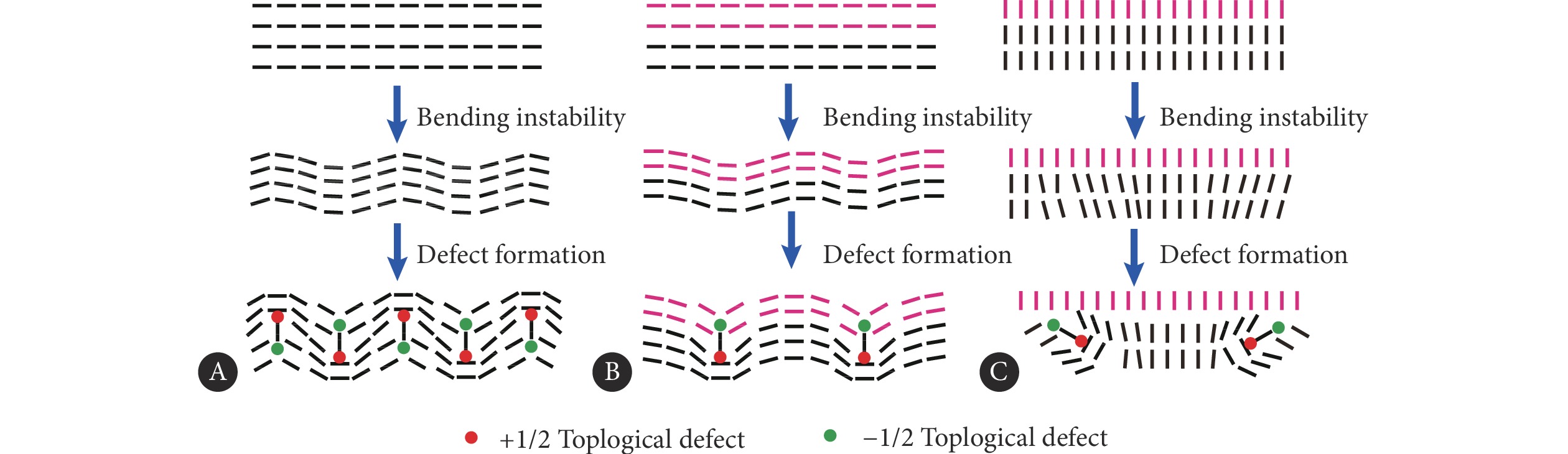
对于内部区域，均匀排列的取向场在活性的作用下发生弯曲失稳，取向场进一步变化之后，最终形成成对的拓扑缺陷，如图8A所示。而在界面处，由于受到界面锚定作用以及系统活性梯度的变化的影响，系统只能沿着特定方向发生失稳。例如，在切向界面锚定的作用下，由于+1/2拓扑缺陷趋向于发生定向迁移，并且只能从界面向高活性区域运动，界面发生局部的扭曲，形成"v"型的尖角，并且在尖角处形成一个−1/2拓扑缺陷，即−1/2拓扑缺陷的结构中，会有两个轴处在界面上，如图8B所示。类似地，对于法向锚定情况，由于锚定作用发生变化，此时缺陷对的形成方向与界面法向有明显的倾角，此时一个−1/2拓扑缺陷中，只有一个对称轴处在界面上，如图8C所示，最终形成多个类似的结构，如图7A所示。因此，这两种界面失稳的模式最终都会促使界面发生−1/2拓扑缺陷聚集，引起负电性能。对于切向锚定，大量的+1/2拓扑缺陷从活性区域向界面区域运动，当到达界面时，+1/2拓扑缺陷驱动能够稳定存在，并驱动界面发生持续变形，此时界面的带电性发生变化。

图  8  缺陷对的形成模式

Figure  8.  Formation patterns of topological defect pairs

A, Active region; B, boundary under tangential anchoring; C, boundary under normal anchoring.

下载: 全尺寸图片 幻灯片

2.4   拓扑缺陷的动力学差异

生物界面的锚定拓扑对界面处的拓扑缺陷的运动行为有着十分显著的影响，尤其是具有自主运动能力的+1/2拓扑缺陷。对于单一的+1/2拓扑缺陷，其运动主要由主动应力$ {{{\sigma}} _{\rm{act}}} = - \overline \zeta {{Q}} $来驱动。缺陷附近的主动力可以表示为：

式(15)中，q表示缺陷附近的序参数幅值，$ \hat {{x}} $表示+1/2拓扑缺陷的极性方向，r表示缺陷核的大小。式(15)表明+1/2拓扑缺陷的推进力主要受两部分因素影响，分别为局部的有序性和活性的大小，即序参数q和平均活性系数$ \overline \zeta $。更强的界面有序性或更强的活性均能够提升+1/2拓扑缺陷的运动能力。当界面锚定与活性锚定协同作用时，和无锚定作用相比，界面处序参数的提高能够使+1/2拓扑缺陷持续驱动界面演化，产生较大的指形结构。

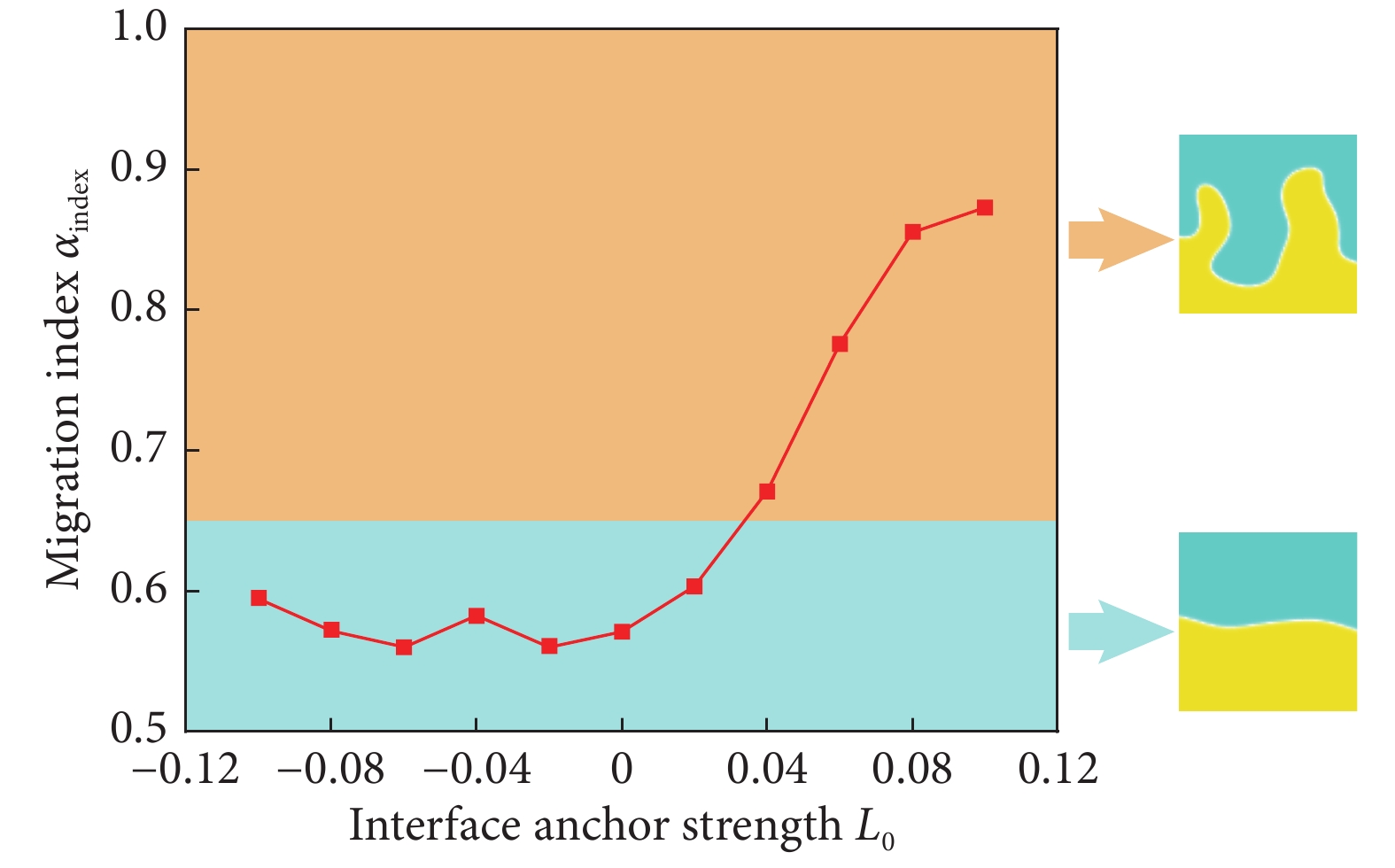
用活性区域的最大宽度与系统整体尺度的比值来定量表征活性相迁移至非活性区域的迁移指数$ {\alpha _{\rm{index}}} $。当指形结构运动占据整个系统尺寸时，即$ {\alpha _{\rm{index}}} = 1 $，活性区域的迁移能力最强，反之当$ {\alpha _{\rm{index}}} = 0.5 $时，系统比较稳定。图9反映了迁移指数$ {\alpha _{\rm{index}}} $随着界面拓扑约束$ {L_0} $的变化情况。计算结果表明，对于拉伸活性的细胞单层，界面的拓扑显著影响细胞向非活性区域远端迁移的能力。对于无锚定系统（$ {L_0} = 0 $），无序界面的序参数值较小，+1/2拓扑缺陷的运动能力较小。因此，指形结构的生长能力很弱，界面稳定。另外，法向锚定能够稳定界面形貌，形成平滑的直界面，迁移指数$ {\alpha _{\rm{index}}} $始终维持较低水平。而对于切向锚定情况，$ {\alpha _{\rm{index}}} $随着锚定强度$ {L_0} $的增强而显著提高。这种作用主要体现在两部分：首先，界面拓扑约束与活性引起的界面排列是协调作用，使得+1/2拓扑缺陷能够稳定存在于界面处；另外，增大序参数能够提高+1/2拓扑缺陷的迁移能力，由于+1/2拓扑缺陷的推动作用是指形结构生长的本质原因，因而细胞的迁移能力显著增强。

图  9  迁移指数$ {\alpha _{\rm{index}}} $随着界面拓扑约束$ {L_0} $的变化情况

Figure  9.  Variation of migration index α_index with interface anchor strength $ {L_0} $

下载: 全尺寸图片 幻灯片

3.   讨论

本文基于数值计算和理论分析相结合的方法，探究了无限大区域内活性-非活性细胞单层界面的形貌动力学。活性-非活性系统提供了界面处的拓扑特征与空间活性非均匀的性质。两相向列系统引起的界面排列约束能够对界面的自组装形貌进行调控，发现了直界面、波浪形界面、指形界面这三种典型的活性-非活性生物界面形貌。

这种边界处的指形结构已经在上皮细胞的二维铺展实验中被发现^{[39, 40-41]}。前人的理论模型通常采用细胞的异质性来实现，即处在边界处的细胞的运动能力更强，且与边界的曲率相关，作为领导细胞带动后面的跟随细胞实现指形结构的生长^[42-44]。本文结果表明，对于均匀的细胞单层系统，界面同样能够形成明显的指形结构，且与界面的拓扑约束有明显的相关性，界面处细胞的切向排列是形成指形结构的重要条件。

由于生物界面的存在，活性区域内部的拓扑缺陷动力学与界面处存在明显的不同。由于内部区域是均匀活性，主要发生拓扑缺陷对的形成与湮灭，并维持动态平衡。而界面是活性与非活性区域的交界处，存在活性系数与取向场的非均匀性，因此，其失稳模式更加复杂。对三种不同界面形貌的取向场进行计算，界面处的带电情况存在显著差异。前人研究已经证明，在活性液晶和各向同性物质的混合系统中，界面带有扩散的负电荷^{[34, 38]}，+1/2拓扑缺陷在驱动界面生长的过程中，到达界面处便会发生融合，界面始终具有负电荷的性质。

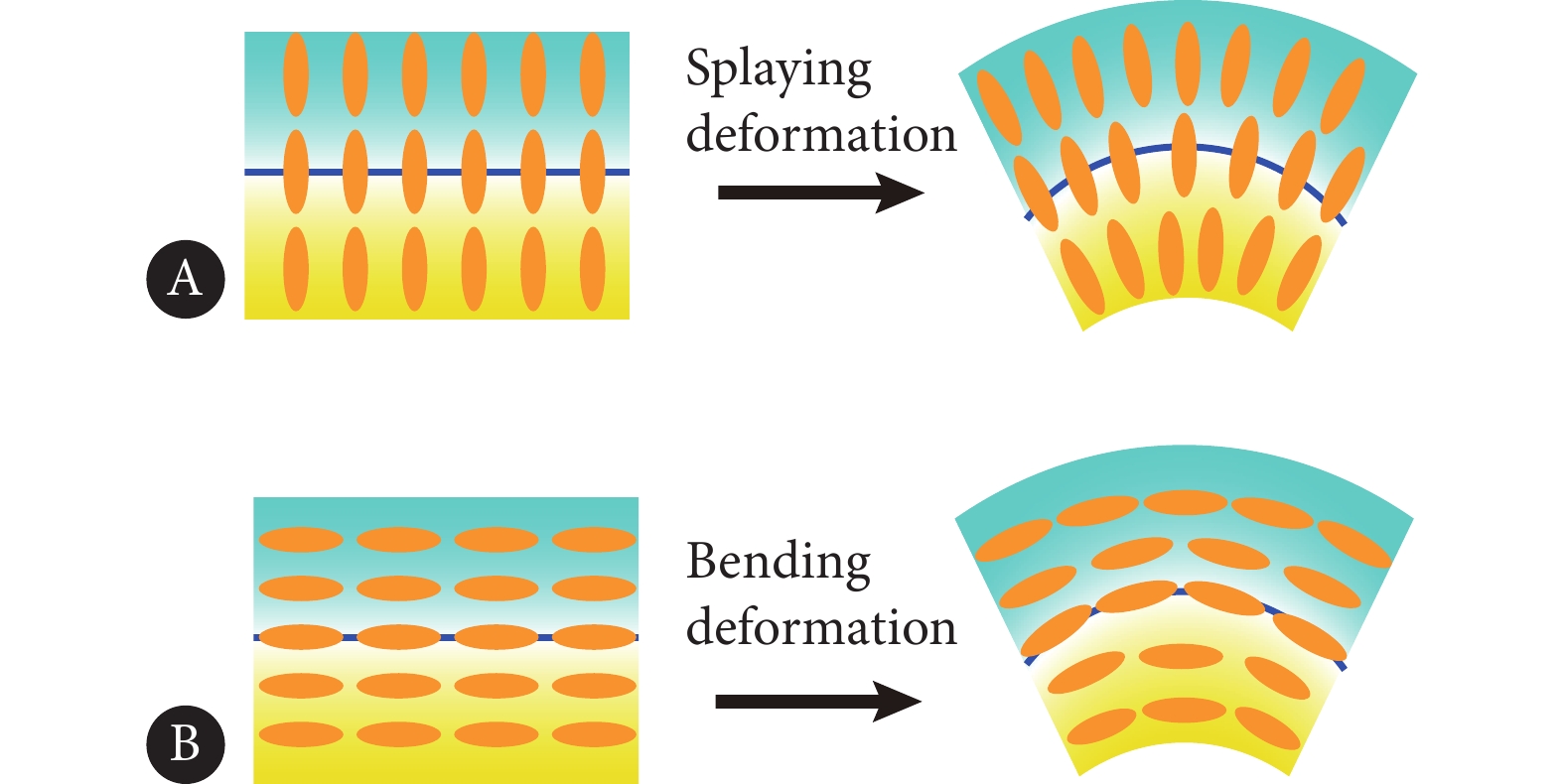
本文中，通过对界面处的拓扑缺陷进行计算发现，三种界面处拓扑缺陷的空间分布模式和运动能力差异显著。无锚定界面的拓扑电荷数趋近于0，界面呈现出不带电的状态；法向锚定的界面能够吸引−1/2拓扑缺陷均匀的排列，界面趋于稳定；切向排列的界面能够吸引更多的+1/2拓扑缺陷到界面，界面上产生指形结构的生长演化。这种界面的取向排列分布对应的液晶失稳模式也截然不同。切向锚定作用下，界面的变形对应取向场发生弯曲变形，如MDCK细胞单层发生的界面失稳；法向锚定作用下，界面的变形对应取向场发生展曲变形，与系统活性导致的失稳模式明显相反，相互竞争，界面处于比较稳定的状态，如图10所示。

图  10  取向场失稳模式

Figure  10.  Instability modes of the orientation field

A, Splaying deformation; B, bending deformation.

下载: 全尺寸图片 幻灯片

本文所关注的活性-非活性界面在生命系统中十分常见，两相组分的活性具有显著差异。类似地，细胞单层的其他的力学性质对其界面行为的影响也同样值得探究，例如细胞单层界面处向列刚度的差异、序参数幅值的差异、细胞黏性的差异等。此外，活性的梯度变化以及活性的空间非均匀性在生命系统中也十分常见，本文所提出的方法可以推广到该类问题中，具有一定的普适性。

*　　　　*　　　　*

作者贡献声明　张德清负责正式分析、调查研究、研究方法、初稿写作和审读与编辑写作，张豪舜负责正式分析、调查研究、初稿写作和审读与编辑写作，李博负责论文构思、经费获取、初稿写作和审读与编辑写作。所有作者已经同意将文章提交给本刊，且对将要发表的版本进行最终定稿，并同意对工作的所有方面负责。

Author Contribution　 ZHANG Deqing is responsible for formal analysis, investigation, methodology, writing--original draft, and writing--review and editing. ZHANG Haoshun is responsible for formal analysis, investigation, writing--original draft, and writing--review and editing. LI Bo is responsible for conceptualization, funding acquisition, writing--original draft, and writing--review and editing. All authors consented to the submission of the article to the Journal. All authors approved the final version to be published and agreed to take responsibility for all aspects of the work.

利益冲突　所有作者均声明不存在利益冲突

Declaration of Conflicting Interests　All authors declare no competing interests.